Tensor computing from scratch part I - Fundamendal operations
Squeeze, unsqueeze, view, reshape, flatten, swapaxes… Oh my! In deep learning applications, tensors can have extremely fluid shapes flowing from one operation to the next. Have you ever wondered how tensor computing libraries such as pytorch, numpy and tensorflow are able to efficiently keep track of your data, weights and activations? Then you’ve come to the right place, as we are going to implement our very own tensor library from scratch!
What are we trying to achieve? Essentially, we want to write a set of functions that work with with tensors, or multi-dimensional arrays, allowing users to perform basic mathematical operations such as summation, multiplication, and so on. This kind of operations are the basis for modern deep learning and artificial intelligence methods, as well as pretty much anything that involves large-scale numerical computations. The numpy documentation has a nice introduction to the basic ideas of working with such type of data.
This post is available as a Jupyter notebook, so feel free to download it and follow along.
Data container
The fundamental idea underlying efficient storage of multi-dimensional arrays is to always keep the data into a simple one-dimensional array, or list. Alongside, we also store the current shape of the tensor and a few more things which we will then use to correctly implement mathematical operations.
Let’s start by implementing the most basic container:
from functools import reduce
from typing import Any, Callable, List, Optional, Tuple
class Tenxor:
def __init__(self, values: List[float], shape: Optional[List[int]]):
self.values = values
if shape is not None:
# the total number of elements must equal the product
# of the size of each dimension
shape_elements = reduce(lambda x, y: x * y, shape)
if len(values) != shape_elements:
raise ValueError(
f"shape {shape} incompatible with values of size {len(values)}"
)
self._shape = shape
else:
self._shape = [len(self.values)]
def get_shape(self) -> List[int]:
return self._shape
def __eq__(self, other: "Tenxor") -> bool:
"""
Two Tenxors are the same if they have the same data and same shape.
"""
return self._shape == other._shape and all(
x == y for x, y in zip(self.values, other.values)
)
def __repr__(self):
vals = ", ".join(map(str, self.values[:5]))
return (
f"{self.__class__.__name__} of {len(self.values)} items"
f" with shape {self._shape} and values [{vals} ... ]"
)
t = Tenxor([0] * 12, [6, 2])
t
Tenxor of 12 items with shape [6, 2] and values [0, 0, 0, 0, 0 ... ]
Pointwise transformations
The simplest kind of operations that we can implement at this point are pointwise transformations, i.e., transformations that involve each element separately.
def ttransform(tenxor: Tenxor, op: Callable[[Any], Any]) -> Tenxor:
"""Transforms all elements of the Tenxor with the given callable."""
return Tenxor([op(x) for x in tenxor.values], tenxor.get_shape())
def tmul_scalar(tenxor: Tenxor, scalar: float) -> Tenxor:
"""Multiplication by a scalar"""
return ttransform(tenxor, lambda x: scalar * x)
def tadd_scalar(tenxor: Tenxor, scalar: float) -> Tenxor:
"""Addition with a scalar."""
return ttransform(tenxor, lambda x: scalar + x)
tadd_scalar(t, 5)
Tenxor of 12 items with shape [6, 2] and values [5, 5, 5, 5, 5 ... ]
Changing shape
Since we keep the tensor shape separate from the actual data, changing shapes is a breeze: we just need to save the new shape somewhere!
The only restriction is that the new shape must imply the same number of elements as the old shape.
For convenience, it is often allowed to use the special size of -1 to indicate that one dimension can take up as many elements as necessary to keep this invariance.
For example, suppose we want to reshape a tensor with shape (6, 2) into shape (-1, 3, 1); the resulting shape would be (4, 3, 1), since it implies the same number of elements.
If would not be possible to reshape (7, 2) into it, however, since you cannot arrange 14 elements into an integer number of rows of 3 elements each.
def tview(old_shape: List[int], new_shape: List[int]) -> List[int]:
"""
Return the new shape of the Tenxor after reshaping.
"""
if any(s < -1 or s == 0 for s in new_shape):
raise ValueError("Zero or negative shape other than -1 not allowed")
# find if there is a dimension of size -1
news = list(new_shape)
fill_dimensions = [i for i, s in enumerate(new_shape) if s == -1]
if len(fill_dimensions) > 1:
raise ValueError("Only one dimension can be -1")
elif fill_dimensions:
# number of elements in the original tensor
numel = reduce(lambda x, y: x * y, old_shape)
# compute the total number of elements implied by the other dimensions
other_ns = reduce(lambda x, y: x * y, (s for s in new_shape if s != -1))
# this number must fit exactly into the total number of elements,
# otherwise it is not possible to pack it into a single dimension
if numel % other_ns != 0:
raise ValueError(f"cannot reshape {old_shape} to {new_shape}")
news[fill_dimensions[0]] = numel // other_ns
return news
assert tview([6, 2], [-1, 3, 1]) == [4, 3, 1]
We now implement two very useful operations to add and remove dimensions of size 1.
These operations are going to be extremely useful later once we implement “broadcasting”, which allows us to work with Tenxors of different shapes.
def tsqueeze(shape: List[int], dim: int) -> List[int]:
"""
Return the new shape of the Tenxor after removing the given dimension of size 1.
"""
if dim < 0:
# support negative indexing from the end
dim = len(shape) + dim
# make sure that the dimension exists and has size 1
if dim < 0 or dim > len(shape):
raise ValueError("shape out of range")
elif shape[dim] != 1:
raise ValueError(f"cannot unsqueeze dimension {dim} of size {shape[dim]}")
# simply remove the given dimension
new_shape = [s for i, s in enumerate(shape) if i != dim]
return new_shape
assert tsqueeze([4, 3, 1], -1) == [4, 3]
def tunsqueeze(shape: List[int], dim: int) -> List[int]:
"""
Add a new dimension of size 1 in the given position.
"""
if dim < 0:
# support negative indexing from the end
dim = len(shape) + dim + 1
if dim < 0 or dim >= len(shape) + 1:
# make sure that the dimension exists
raise ValueError("shape out of range")
# add a new dimension of size 1 in the right place
new_shape = shape[:dim] + [1] + shape[dim:]
return new_shape
assert tunsqueeze([4, 3], 0) == [1, 4, 3]
assert tunsqueeze([4, 3], -1) == [4, 3, 1]
Element indexing
The key issue that we need to solve before moving on to more complex operations is to index the elements contained in a tensor.
Here, I do not mean indexing with brackets as in t[0, 1, 2], but rather finding the position in the flattened item array corresponding to a certain multi-dimensional index.
This is where knowing the shape becomes crucial.
Suppose that we are working with a two-dimensional array of shape (5, 3). It is natural to put the element (0, 0) at position 0 of the flat array.
Now, we are going to assume that the last dimension is the fastest that changes, so that the element (0, 1) goes into position 1, and the element (0, 2) to position 2.
The second-to-last dimension is the next one to change, so that (1, 0) goes to position 3, (1, 1) to position 4, and so on.
Generally, the item (a, b) of a (5, 3) array goes to position 3 * a + b.
With more dimensions, we simply need to multiply the index with the shape of all previous dimensions combined.
def position_to_index(pos: List[int], shape: List[int]) -> int:
"""
Find the index in the flattened array corresponding to the given
position in the multi-dimensional tensor.
"""
idx = 0
acc = 1
k = len(shape) - 1
while k >= 0:
if pos[k] >= shape[k]:
raise RuntimeError(
f"index {pos[k]} at dimension {k} out of bounds for size {shape[k]}"
)
idx += acc * pos[k]
acc *= shape[k]
k -= 1
return idx
assert position_to_index(pos=[1, 2, 3], shape=[5, 6, 7]) == 59 # = 3 + 2*7 + 1*7*6
We will also need a function for the inverse operation, i.e., mapping an index into the flat array back to an index into the multi-dimensional tensor.
In our running example, a flat index of 4 for a shape of (5, 3) should be mapped to position (1, 2) since 4 = 1 * 3 + 2.
In the following function, I use the term “slice” to indicate the elements of the flat array spanned by each dimension of the tensor.
In other words, which and how many elements should be skipped each time the index of that dimension is incremented by one.
The very last slice always has size one, since incrementing the last index moves the index into the flat array by one.
The second-to-last slice has size equal to the last dimension: in our (5, 3) example, the element (1, 2) is separated from the element (0, 2) by exactly three elements.
In a tensor of shape (5, 6, 7), the slices have size (42, 7, 1), where 42 = 7 x 6.
This means that the elements (i, j, k) and (i + 1, j, k) are separated by 42 elements in the flattened array.
Suppose we want to find the multi-dimensional position of element 59 in the flattened array:
- Because 42 divides 59 one time with remainder of 17, the first dimension has index 1.
- The remaining 17 items are divided by 7 two times with remainder 3, so the second dimension has index 2.
- The remaining 3 items are divided by 1 3 times with remainder 0, so the third dimension has index 3.
def index_to_position(idx: int, shape: List[int]) -> int:
"""
Finds the position in the multi-dimensional tensor corresponding to
the element at the given index in the flattened array.
"""
# we could make this function more efficient by pre-computing this
# and storing it in the Tenxor
slice_sizes = [1] * len(shape)
for k in range(len(shape) - 1, 0, -1):
slice_sizes[k - 1] *= shape[k] * slice_sizes[k]
pos = [0] * len(shape)
for k in range(len(shape)):
pos[k] = idx // slice_sizes[k]
idx = idx % slice_sizes[k]
if pos[k] >= shape[k]:
raise RuntimeError(
f"index {pos[k]} at position {k} out of bounds"
f" for slice size {slice_sizes[k]}"
)
return pos
assert index_to_position(59, [5, 6, 7]) == [1, 2, 3]
Finally, the last foundational method we need is one to find the position that is immediately “following” a given position. With this method, we will be able to navigate a tensor visiting all its elements one after the other, thus building a fundation for complex binary operations between two tensors.
def next_position(pos: List[int], shape: List[int]) -> bool:
"""
Find the multi-dimensional position immediately "after" the given position.
Modifies `pos` in place, returns true if there are more elements to visit,
or false if the computed position is out of bounds.
"""
pos[-1] += 1
k = len(pos) - 1
while k > 0 and pos[k] == shape[k]:
pos[k] = 0
pos[k - 1] += 1
k -= 1
return pos[0] < shape[0]
p = [1, 2, 6]
next_position(p, [5, 6, 7])
assert p == [1, 3, 0]
Let’s make sure that these methods can work together harmoniously by scanning all elements of a tenxor and ensuring that these methods give consistent results:
pos = [0, 0, 0] # initial position
shape = [2, 2, 2] # shape of the tenxor
has_more = True
idx = 0
while has_more:
print(f"Index {idx} corresponds to position {pos} for shape {shape}")
assert pos == index_to_position(idx, shape)
assert idx == position_to_index(pos, shape)
has_more = next_position(pos, shape)
idx += 1
print(f"First position out of bounds for shape {shape} is {pos}")
Index 0 corresponds to position [0, 0, 0] for shape [2, 2, 2]
Index 1 corresponds to position [0, 0, 1] for shape [2, 2, 2]
Index 2 corresponds to position [0, 1, 0] for shape [2, 2, 2]
Index 3 corresponds to position [0, 1, 1] for shape [2, 2, 2]
Index 4 corresponds to position [1, 0, 0] for shape [2, 2, 2]
Index 5 corresponds to position [1, 0, 1] for shape [2, 2, 2]
Index 6 corresponds to position [1, 1, 0] for shape [2, 2, 2]
Index 7 corresponds to position [1, 1, 1] for shape [2, 2, 2]
First position out of bounds for shape [2, 2, 2] is [2, 0, 0]
This basic loop and its variations will form the basis by which we implement many operations later, so be sure to understand how it works!
Tensor interface
We want to hide the fact that the data is stored in a simple list, so that users of our tensors can use it only via multi-dimensional indexing. Therefore, let us create a basic class that defines the interface by which we will use the tensors, plus a few simple operations:
class AbstractTenxor:
# abstract interface
def get_shape(self) -> List[int]:
raise NotImplementedError()
def get_at_position(self, pos: List[int]) -> float:
raise NotImplementedError()
def set_at_position(self, pos: List[int], val: float) -> None:
raise NotImplementedError()
def next_position(self, pos: List[int]) -> bool:
raise NotImplementedError()
def transform_values(self, op: Callable[[float], float]) -> "AbstractTenxor":
raise NotImplementedError()
# shape features
def squeeze(self, dim: int) -> "AbstractTenxor":
new_shape = tsqueeze(self.get_shape(), dim)
return self.view(new_shape)
def unsqueeze(self, dim: int) -> "AbstractTenxor":
new_shape = tunsqueeze(self.get_shape(), dim)
return self.view(new_shape)
def view(self, shape: List[int]) -> "AbstractTenxor":
raise NotImplementedError()
And provide an implementation of these methods for the basic container above:
class Tenxor(AbstractTenxor):
def __init__(self, values: List[float], shape: List[int]):
self._values = values
self._shape = shape
def get_shape(self) -> List[int]:
return self._shape
def view(self, shape: List[int]) -> "Tenxor":
return Tenxor(self._values, shape)
def get_at_position(self, pos: List[int]) -> float:
idx = position_to_index(pos, self._shape)
return self._values[idx]
def set_at_position(self, pos: List[int], val: float) -> None:
idx = position_to_index(pos, self._shape)
self._values[idx] = val
def next_position(self, pos) -> bool:
return next_position(pos, self._shape)
def transform_values(self, op: Callable[[float], float]) -> "Tenxor":
return Tenxor([op(x) for x in self._values], self._shape)
def __eq__(self, other: "Tenxor") -> bool:
return self._shape == other._shape and all(
x == y for x, y in zip(self._values, other._values)
)
This structure will become useful in part 2 of this series, as we are going to provide new tensor implementations with additional features.
Reduction along one axis
Finally we can start with actual maths! There are two fundamental operations that we should support: reduction along one axis, and pointwise operations between elements at the same position. More complex operations can be implemented on top of these two as we are going to see later.
Let’s start with reduction. The goal here is to combine all elements that belong to a given dimension of the array, e.g. by summing them. For example, since rows are the first dimension of a matrix, a reduction along the first dimension combines all elements of each column together, and the result is an one-dimensional array with one element for each column. A reduction along the second axis works in the opposite way, combining the elements of each row.
You can think of the dimension that we reduce along as the dimension that “disappears” in the result.
For example, reducing an array of shape (4, 3, 2) along the second dimension results in an array of shape (4, 2).
The element at position (3, 1) of the result is obtained by combining the elements at positions (3, 0, 1), (3, 1, 1) and (3, 2, 1) of the input array.
def tredux(
tenxor: AbstractTenxor, dim: int, init: Any, redux: Callable[[Any, Any], Any]
) -> AbstractTenxor:
"""
Combine all elements of the given dimension using the operation provided.
"""
if dim < 0:
dim = len(tenxor.get_shape()) + dim
if dim < 0 or dim > len(tenxor.get_shape()):
raise ValueError("shape out of range")
# Compute the shape of the result and initialize its elements.
# At first we keep the dimension that we are reducing along, but with
# only one element that contains the result along that slice.
# initialize the result tensor
res_shape = [s if i != dim else 1 for i, s in enumerate(tenxor.get_shape())]
result = Tenxor([init] * reduce(lambda x, y: x * y, res_shape), res_shape)
# initialize the counters
res_pos = [0] * len(res_shape)
res_has_more = True
while res_has_more:
# scan the input tensor along the given dimension and reduce all items there
in_pos = res_pos[:]
acc = init
for i in range(tenxor.get_shape()[dim]):
in_pos[dim] = i
acc = redux(acc, tenxor.get_at_position(in_pos))
result.set_at_position(res_pos, acc)
# move to next result position
res_has_more = result.next_position(res_pos)
# finally remove the dimension that we reduced along
return result.squeeze(dim)
tx = Tenxor(range(24), (4, 3, 2))
# sum all elements of the first dimension
assert tredux(tx, 0, 0, lambda x, y: x + y) == Tenxor([36, 40, 44, 48, 52, 56], [3, 2])
# sum all elements of the second dimension
assert tredux(tx, 1, 0, lambda x, y: x + y) == Tenxor(
[6, 9, 24, 27, 42, 45, 60, 63], [4, 2]
)
# sum all elements of the third dimension
assert tredux(tx, 2, 0, lambda x, y: x + y) == Tenxor(
[1, 5, 9, 13, 17, 21, 25, 29, 33, 37, 41, 45], [4, 3]
)
Note that in this function we visit each item of the result only once and reduce all input elements in one shot with the inner loop. The other option would be to scan each item of the input, figure out where it should end up in the result, and perform the computation accordingly, thus eliminating the need for an inner loop. The reason why we did it in this way is that it would be much easier to parallelize, for example on a GPU, since we could have in principle a thread for each item of the result, and all these threads could write independently of each other (having multiple threads writing to the same location is much slower since they would need to synchronize).
Pointwise operations
Pointwise operations combine the elements of two input tensors that are located at the same position. When the two tensors have the same shape everything is easy, but the real power of this function comes from combining tensors of different sizes. How is it possible you ask? This is thanks to broadcasting, which is a fundamental concept to write more complex numerical routines.
Let’s start with an example: the outer sum between a vector of size 4 and a vector of size 3, matrix of size (4, 3).
The element at position (i, j) of this matrix comes from the sum of element i of the first vector and element j of the second vector.
But we want to compute this as the combination of two tensors of the same shape, so how can we get this result by adding together the elements at position (i, j) of two matrices of size (4, 3)?
Well, we could take the fist vector of size four, and create three copies of it along three columns of one matrix, then take the second vector of size three and create four copies of it along two rows of the second matrix, like this (image from the numpy documentation):
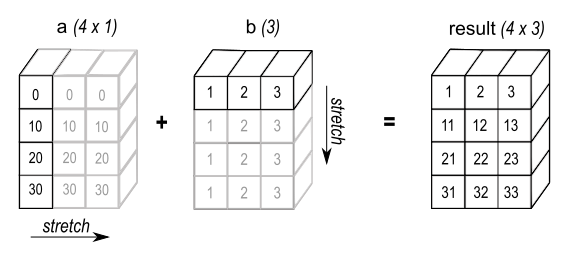
This is essentially the core of broadcasting: we create copies of certain dimensions of the two input arrays, or “stretch” them, such that all of their dimensions match. To make this efficient, we do not want to actually copy the data, we would rather work with the two inputs as they are.
Not all inputs can be broadcasted together, however; their shapes have to be compatible.
In general, two vectors can be broadcasted together as long as their shapes can be paired such that the sizes of each dimension are the identical, or one of them equals 1.
For example, (5, 1) can be broadcasted with (5, 3).
Moreover, if one array has fewer dimensions, its shape can be extended to the left with additional dimensions of size 1; for example, (5, 1, 3) can be broadcased with (4, 3), since the latter shape can be extended to (1, 4, 3), and the result would have shape (5, 4, 3).
You can visualize this easily by writing the shapes and aligning each dimension of the inputs to the right:
(5, 1, 3) # Shape of a
( 4, 3) # Shape of b
(5, 4, 3) # Shape of c = a + b
The actual computation performed is:
c = a + b
# c[i, j, k] = a[i, 0, k] + b[0, j, k]
The way to understand indexing is that an index for a dimension is not used for an input whenever its size is one, using 0 instead.
Since the second dimension of a has size 1, then the second dimension of the result does not come from a, i.e., the index j is not used for a.
In the same way, since the first dimension of b is 1 after broadcasting, the first index of the result, that is i, is not used to index c.
This is exactly how we are going to implement broadcasting: ignore indices corresponding to dimensions of size 1.
Feel free to check numpy’s documentation on broadcasting for more detailed explanation and examples.
def broadcast_shapes(
shape_a: List[int], shape_b: List[int]
) -> Tuple[List[int], List[int], List[int]]:
"""
Broadcast the shapes of two tensors, returning the new shapes after broadcasting as well
as the shape of the result.
"""
# match the length of the shapes by extending
# the shorter one with ones to the left
an, bn = len(shape_a), len(shape_b)
if an == bn:
pass
elif an > bn:
shape_b = [1] * (an - bn) + shape_b
elif an < bn:
shape_a = [1] * (bn - an) + shape_a
# check that shapes are compabible, and compute the shape of the result
result_shape = []
for k, (n, m) in enumerate(zip(shape_a, shape_b)):
r = None
if n == 1:
# dimension k of the first tensor is broadcasted
# use dimension k of the second tensor as
# size for this dimension of the result
r = m
elif m == 1:
# dimension k of the second tensor is broadcasted
# use dimension k of the first tensor as
# size for this dimension of the result
r = n
elif m != n:
# input tensors have different shapes that are not broadcastable,
# i.e., different than one
raise ValueError(
f"incompatible shapes {shape_a} and {shape_b} at dimension {k}"
)
else:
r = m
result_shape.append(r)
return shape_a, shape_b, result_shape
assert broadcast_shapes([5, 1, 3], [7, 1, 4, 3]) == (
[1, 5, 1, 3], # dimension of size one added to the right of shape_a
[7, 1, 4, 3], # shape_b remains the same
[7, 5, 4, 3], # dimension of the result with the largest size for each axis
)
We can now use this function to align the shapes of the two tensors and compute the result shape before doing the point-wise operation:
def tpoint(a: Tenxor, b: Tenxor, redux: Callable[[Any, Any], Any]) -> Tenxor:
"""
Perform a pointwise operation by combining the two elements of the inputs
that are in the same position after broadcasting.
"""
# broadcast tensors and compute shape result
a_shape, b_shape, result_shape = broadcast_shapes(a.get_shape(), b.get_shape())
a_broad = a.view(a_shape)
b_broad = b.view(b_shape)
# initialize the container data for the result tensor and the position cursor
result = Tenxor([None] * reduce(lambda m, n: m * n, result_shape), result_shape)
result_pos = [0] * len(result_shape)
result_has_more = True
# perform the operation
while result_has_more:
# find the positions in the input arrays:
# use 0 in each dimension that was broadcasted
pos_a = [i if n > 1 else 0 for i, n in zip(result_pos, a_broad.get_shape())]
pos_b = [i if n > 1 else 0 for i, n in zip(result_pos, b_broad.get_shape())]
# perform the operation, store the result and move on
res = redux(a_broad.get_at_position(pos_a), b_broad.get_at_position(pos_b))
result.set_at_position(result_pos, res)
result_has_more = result.next_position(result_pos)
return result
assert tpoint(
Tenxor([1, 2, 3], (3, 1)),
Tenxor([1, 2, 3], (1, 3)),
lambda x, y: x * y, # element-wise product
) == Tenxor([1, 2, 3, 2, 4, 6, 3, 6, 9], [3, 3])
The operation above computed the outer product of $\vert 1, 2, 3 \vert$ as a column vector with its transpose, i.e. a row vector, giving a 3 by 3 matrix:
\[\begin{vmatrix} 1 \\ 2 \\ 3 \end{vmatrix} \times \begin{vmatrix} 1 & 2 & 3 \end{vmatrix} =\begin{vmatrix} 1 & 2 & 3 \\ 4 & 6 & 8 \\ 3 & 6 & 9 \end{vmatrix}\]If you are short on time, this is the bare essential to know on tensor computing from scratch!
But if you are thirsty for more, including the implementation of a graph neural network, transpositions, and slicing, hang on for part 2 of this series!