Best time to buy and sell stocks
There is a problem on LeetCode that goes like this: “You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock. Find the maximum profit you can achieve from this transaction.” Where we can decide to sell “in the past” to maximize the profit. Finding the solution and why it works took me way too much effort (spoiler alert).
I have to admit, I only found the solution because I thought at a similar problem (finding the subarray with the largest sum) we studied in the class on algorithms and data structures during my bachelor’s degree. And I also have to admit, I was equally bewildered at that time.
Anyways, in this problem we are given the list of prices and we have to find the maximum possible profit we could achieve by buying at some point and selling after that point. The solution is surprisingly simple:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
best = 0
i = 0
j = 1
while j < n:
profit = prices[j] - prices[i]
if profit > best:
best = profit
elif profit < 0:
i = j
j += 1
return best
As an aside, it does not look very Pythonic because it’s written to be fast. In fact, this is in the top 8% fastest solutions (I also have no clue how to make it faster). A more stylish version would be something like this:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
best = i = 0
for j, x in enumerate(prices):
profit = x - prices[i]
best = max(best, profit)
if profit < 0:
i = j
return best
But this is only in the top 20%.
So how does this work? We keep two cursors, i and j, corresponding to the times we buy and sell the stock.
We use j to go forward in time, computing on every new day the profit we would make and if necessary updating the highest profit yet.
So far so good, but then what happens is pretty weird: if we find a negative profit, we decide to restart buying today (at day j)!
How on earth does this make sense?
Imagine we are in this situation:
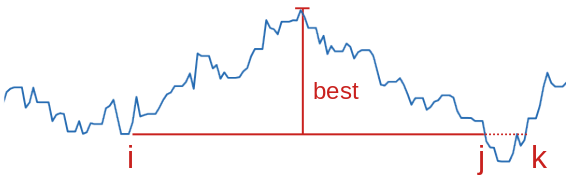
Then, you understand, moving forward with j but not with i will generate negative profits for a while.
For sure, at some point we will reach a point of time k where the price has recovered to the same level as day i, but we could also have bought the stock in the dip between j and k and maybe that’s where the maximum profit will be!
The key to understand the solution is that if we find a point in the future (after k) with better profits than the current best, we could make even more money by shifting i to the dip between j and k.
Look:

Imagine we found a new best at time j', then clearly a better solution would be with i starting at the lowest point between j and k, and this is the purpose of the i = j statement.
Importantly, i will always be at the bottom of a dip: the price immediately preceding i will be greater than or equal to it and the price immediately following i will be greater than it.
Why?
Because as long as prices keep going down (generating negative profits), i follows j until it gets to the bottom of the dip.
Then, as soon as prices go up (generating positive profits), i will stay in the dip and j will move until it gets back down to the price at day i, at which point i follows j again to the bottom of the new dip.
I hope that writing this down will help me (and you!) remember this type of reasoning for the next similar problem. Feel free to apply this idea to the maximum subarray problem if you haven’t already, happy (leet)coding!