Orange Slices
I found an interesting geometrical riddle on Twitter that I could not ignore. After I read the first few chapters of “The art of problem solving” I wanted to challenge myself, and this turned out to be a very nice problem with a neat solution.
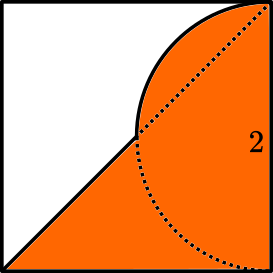
This is the problem, from this Tweet
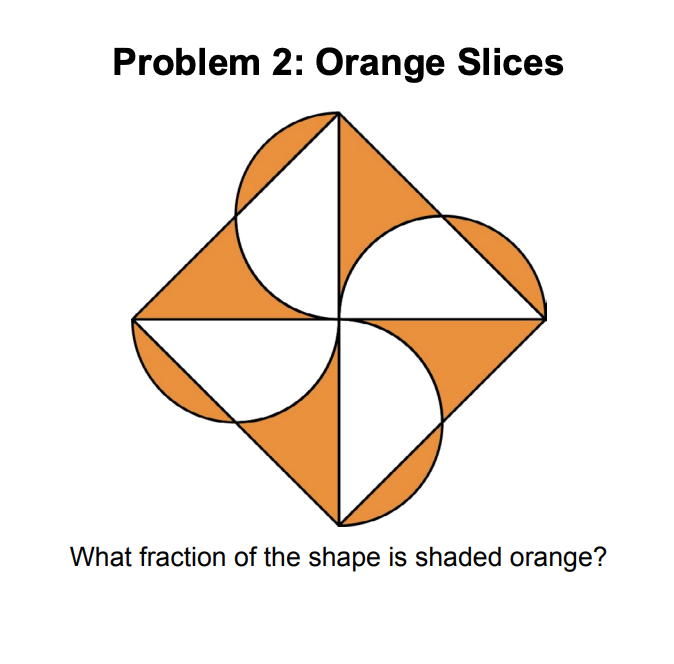
A good strategy to approach this kind of riddles is to look for simmetries. It is clear that the image above is made of four identical pieces that look like this:

Since the question asks for the fraction of shaded area, we can find the answer by focusing only on this picture above. To find the fraction of shaded area, we need to divide the dark orange area by the total colored area in the picture below:

We can find the dark area by noticing what happens when you reflect that circular segment in the top right corner. It will exactly cover the “hole” created by the circle on the opposite side:
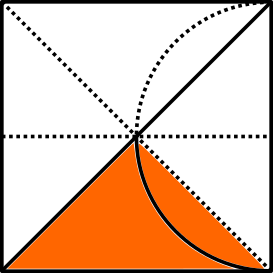
Therefore, the dark area is one fourth of the area of the outer square. Assuming that the side is 2 (later it will be clear why), the orange area above is $2^2/4=1$.
Let’s now focus on finding the total area of the figure. For this, we need to figure out how big that circular segment is.
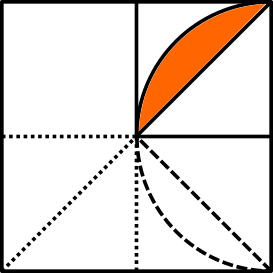
Looking again for symmetries, we see:

Which allows us to compute the orange area above as the difference between the area of the circle and that of the inner square. Assuming that the radius of the circle is 1, its area is $\pi$. This also gives that the diagonal of the square is 2, meaning that its side is $\sqrt{2}$ and its area is 2. This means that each of the four shaded circular segments has area $\frac{\pi-2}{4}$:
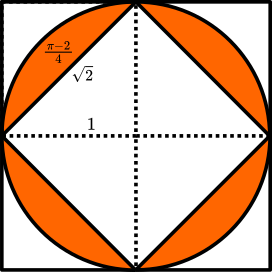
Putting everything together, we find that the total area is $\frac{\pi-2}{4}+2$, which is the sum of the area of the circular sector and half the outer square:
We can finally answer the riddle. The fraction of shaded area is:
\[\frac{1}{\frac{\pi-2}{4}+2}=\frac{1}{\frac{\pi-2+8}{4}}=\frac{4}{\pi+6}\]